This year I took part in Summer of Bitcoin (SoB) [1], which is an online intership aimed at university students to promote bitcoin open source development. My contribution was a project called Efficient Min Convex Cost Flow Solver for Lightning Network Payment Delivery, proposing the design and implementation of a C++ mini-library with no external dependencies for solving the minimum cost flow problem (MCF) with convex costs that can be used to assist Pickhardtpayments to compute optimal payment routes in the Lightning Network.
My mentor, Rene Pickhardt, is the main developer of Pickhardtpayments a python package. His idea consist in representing the Lightning Network as an Uncertainty Network, ie. partial knowledge about the location of every channel liquidity is recorded, updated and used to compute the probability of success of payment routes. A Multi-part payment in this model is represented as a flow in the Uncertainty Network with an associated cost which is a linear combination of the payment fees and \(- \log P\) where \(P\) is its probability of success. Finding a minimum-cost flow would then be equivalent to choosing a set of payment routes that reduces the fees and the probability of failure for lack of funds along the selected routes. The feedback of the LN after every payment routing attempt is used to update the knowledge in the uncertainty network. The process of computing the optimal MPP, make routing requests and network update repeats until all the payment has been delivered or the algorithm determines that there are no routes with sufficient liquidity. See the original paper Pickhardt-Richter 2021 [2] for details and the source code of the package on github [4]. Also a summary of the main ideas of his paper can be found in another blog post [3].
From convex to linear cost functions
For the limited time available to carry out this summer project we decided to solve the Convex Cost Flow problem by using a piecewise linear approximation of the cost function that effectively transforms the original problem into a Minimum Linear-Cost Flow problem for which a variety of efficient algorithms are very well known.
Formally, let \(G(V,E)\) be the directed graph constituted by the node set \(V\) and arcs set \(E\), and let \(u\colon E \to R\) be the arc capacities and for every \(e\in E\) the cost function be denoted as \(c_e\colon [0,u(e)] \to R\). One can always split the domain into \(n\) pieces, for instance \([d_e^0,d_e^1]\), \([d_e^1,d_e^2]\), …, \([d_e^{n-1},d^n_e ]\), with \(d_e^0 = 0\) and \(d_e^n = u(e)\); and introduce a new set of \(n\) arcs \(\{ e^k \}_{k=1,...,n}\) sharing the same endpoints as \(e\), but with capacities \(u(e^k) = d^k_e - d^{k-1}_e\) and linear cost function \(c_{e^k}(x) = m_{e^k} x\), where \(m_{e^k} = \frac{c_e(d^k_e)-c_e(d^{k-1}_e)}{u(e^k)}\) is the mean slope of \(c_e\) in the range \([d_e^{k-1},d_e^{k}]\).

A flow \(x\) passing through \(e\in E\) will be decomposed into \(n\) fractions of flow \(y^k\) that will be distributed among the new linear cost arcs \(e^k\).
\[y^k = \begin{cases} 0 & x < d_e^{k-1} \\ x - d_e^{k-1} & d_e^{k-1} \le x < d_e^k \\ d^k_e - d^{k-1}_e & x \ge d_e^k \end{cases}\]With these constraints we obtain
\[x = \sum_{k=1}^n y^k\] \[c_e(x) = \sum_{k=1}^n c_{e^k}(y^k) = \sum_{k=1}^n m_{e^k} y^k\]Only if the cost function \(c_e\) is convex we are ensured that the optimal splitting of the flow \(x\) among the \(e^k\) sub-arcs will satisfy the previous constraints. This is shown in section 14.4 of Ahuja 1993 [5].
A Tailored Minimum Cost Flow Solver
Pickhardtpayments package [4] already takes the gossip information from the Lightning Network and builds the Uncertainty Network, Then for every payment request, the package feeds into the MCF solver the piecewise linearized-cost network.
When this project SoB project was proposed, Pickhardtpayments was using Google’s OR-Tools library [6] to solve the MCF problem. That MCF solver is based on one of the most efficient in practice algorithm there exists for MCF, called cost-scaling, see [7] for the original paper. However, the lack of an API in OR-Tools to update the costs of the arcs, leads inevitably to the requirement that OR-Tools’ graph must be constructed and initialized with cost and capacities values everytime a MCF computation is demanded in Pickhardtpayments. It would be preferable to have instead a MCF solver that allows for the update of the cost/capacity function of selected arcs. It turned out that the time spent feeding the data into OR-Tools, typically 1 second for the LN, exceeded 3-fold the time spent in computation. Hence it would be preferable to implement a tailored solver for our problem data that would allow lightweight arcs updates between steps of the Pickhardtpayments.
My work during SoB consisted in the development of a MCF solver (see my github repository [8]) with an API designed to match the data requirements of Pickhardtpayments and avoid wasteful use of resources.
The final product of the library is a object called MCFNetwork,
accessible from C/C++ and Python, that exposes all the necessary methods to
construct or update the graph of the problem, find the optimal flow and retrieve the results.
There are myriad of algorithms for solving the MCF problem and some of them are very complex. During the development of the library I’ve tried several MCF algorithms to compare their performance at the end of the development process. They are:
- The pseudo-polynomial Augmenting-paths (also known as Successive shortest path) with complexity \(O(nU)\), section 9.7 of Ahuja [5].
- The pseudo-polynomial Primal-dual with computational complexity \(O(\min(n U, nC))\), section 9.8 of Ahuja [5].
- The weakly-polynomial, Cost-scaling with complexity \(O(n^2 m \log(n C))\), section 10.3 of Ahuja [5].
In practice the performance of MCF algorithms could vary depending on the topology of the graph and the particular aspects of the implementation (for example the data structures to represent adjacency). For that reason it made sense to first gather a good deal of textbook MCF solvers and compare their performance with random graphs and ultimately find which of these algorithms perform best for the particular problem we are trying to solve.
In order to test the penalties in performance due to the use of complicated dynamic data structures to store adjacency relations and nodes/arcs external ids, I have also written a 4th solver based on cost-scaling but using satic data, that means that the number of nodes and arcs of the graph are know at construction and they remain unchanged until the end.
Figure 2 shows the benchmarks we have run to test the solves we have implemented in our library.
These test were produced with random graphs generated using networkx’s
[10] function gnm_random_graph which produces
a random graph with \(N\) nodes and \(M\) arcs.
The number of arcs \(M\) was fixed to \(\lfloor 7.5 N \rfloor\),
which is approximately the relationship
between nodes and channels in the Lightning Network.
We had changed the number of nodes \(N\) from \(2^7 =128\) until
\(2^{14} \approx 16000\) and for each value of \(N\) we generated 40 random graphs.
Costs and capacities for arcs were selected as random numbers from 0 to 200.
In the plot we show the maximum runtime employed by the solvers to find a MCF solution
for all 40 test cases for each value of \(N\).
The lines labelled Augmenting-path, Primal-dual and Cost-scaling correspond to
to the three solves provided in our library that can handle dynamic graph data.
While the line Cost-scaling-simple represents the solver we have written with static graph data.
The runtime of the OR-tools’s solver is also tested as baseline.
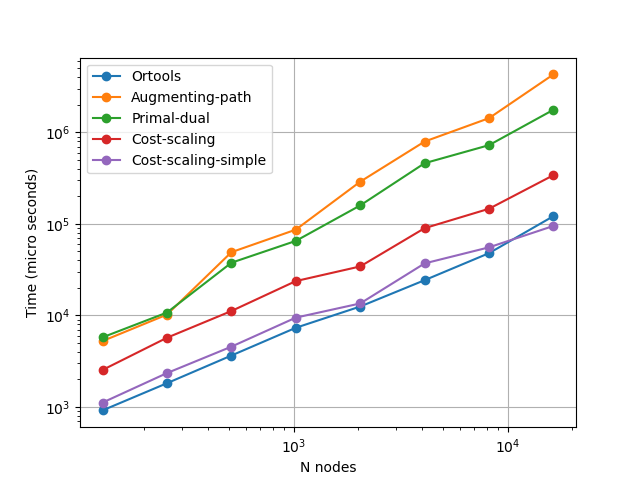
From the results shown in Fig. 2 it can be seen that the 3 best runtimes for all values of \(N\) are those from the solvers that use the cost-scaling algorithm. Just like theory predicts, cost-scaling is very efficient at solving the MCF problem and superior to pseudo-polynomial algorithms. We also learnt that there is, as we had expected, an overhead in our implementations that use dynamic graphs, we can notice by the fact that Cost-scaling-simple is 3 times faster than Cost-scaling, even though they are both using the same algorithm. The benchmarks also reveal that our implementation of cost-scaling, besides the overhead introduced by the dynamic graph, is near optimal as Cost-scaling-simple has runtimes similar to OR-tools’ solver.
Results
I’ve finally integrated my library into the the pipeline of Pickhardtpayments. The process is documented in this pull request [11]. After adapting the API of my library to the use case of Pickhardtpayments I could run further benchmarks, this time simulating payments performed in the Lightning Network using Pickhardtpayments.
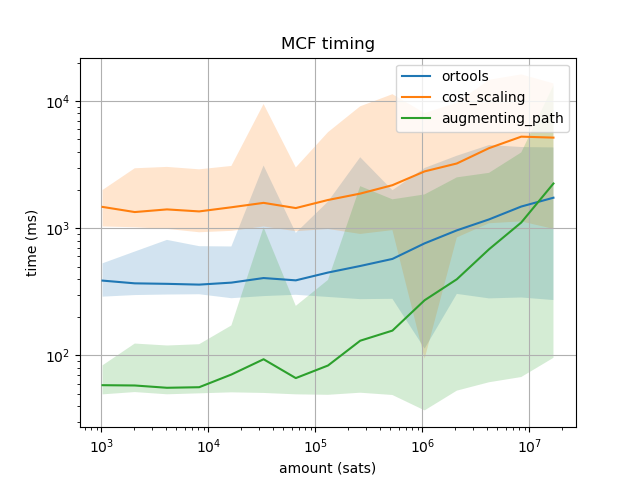
For these benchmarks, each test case consists of a random pair of nodes from the Lightning Network \((A,B)\) and a certain amount \(s\) of satoshis to be sent from \(A\) to \(B\). The pairs are selected from a population of pairs for which a feasible solution exists. Several values of \(s\) were tested from \(2^{10}\) until \(2^{24}\), and for each value of \(s\) we have generated 100 pairs of nodes.
The first plot shows the time spent in computing the MCF for three backends: Google’s OR-tools and two MCF solvers from my library using cost-scaling and augmenting-path. The lines indicate the mean value of the runtime and the shaded regions indicate the maximum and minimum runtime of the testcases. It is noteworthy that OR-tools and my cost-scaling solver have the same curve shape, which is expected since they both consist of the same algorithm, however OR-tool runtime is roughly 3 times faster than my own implementation. On the other hand, my implementation of augmenting-path can be almost a factor of 10 faster than OR-tools for small transactions, though the runtime increases faster than cost-scaling with the amount, going above OR-tools curve for transactions of 16M sats. This result is counter-intuitive since we had already tested for random graphs that cost-scaling was for every graph size always order of magnitude faster than augmenting-path. However, topology matters, and the experiment have shown that for the current topology of the Lightning Network, for small payment amounts the augmenting-path approach is better than cost-scaling.
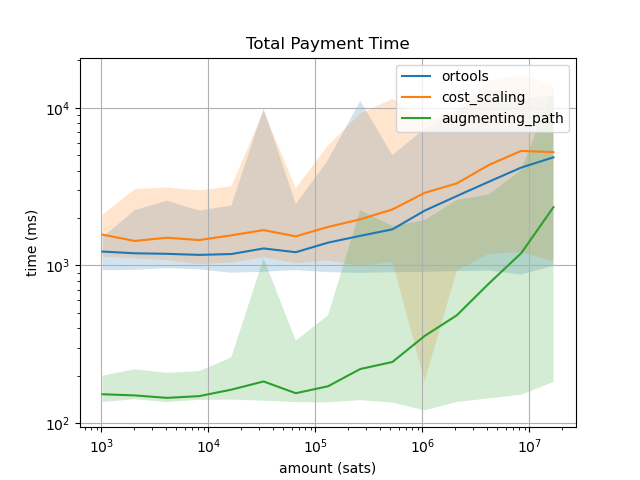
The second plot is possibly the
most important result of our work.
Our MCF solver, being tailored specifically
for the Lightning Network, has the advantage that between iterations of Pickhardtpayments when the
uncertainty network is updated the MCF data structure MCFNetwork needs only to update the
corresponding arcs and not build the entire graph as it was done with the external OR-tools library.
For that reason, the initialization of the object MCFNetwork, which is a resource expensive
operation, only takes place when the “server” starts and between payments it only needs to be
updated. Combining this optimization with the augmenting-path solver we are able to ensure that the
computation of the payments falls below 1 second for transactions up to 1M sats.
Future perspectives
Considering the results of the benchmarks and the current state of this project, there remain major branches to work on:
-
We must improve the runtime of our cost-scaling implementation and add a triggering mechanism to our default solver so that we can use cost-scaling for payments above 10M sats where the algorithm would perform better than augmenting-path. We could achieve a better cost-scaling performance by reducing the overhead caused by the adjacency abstraction in our implementation and another possibility will be the use of the heuristics described in Goldberg 1997 [9].
-
Investigate other algorithms with different complexities. For example cycle-cancelling and double-scaling, as well as other solutions that would not require the piecewise linear approximation to solve the minimum convex-cost flow.
-
Write the uncertainty network code and payment session in C/C++ for better performance.
-
Port this package ideas to a Lightning Network Development Kit to put it into practice.
Conclusions
For the Summer of Bitcoin 2022, I’ve been working on a Minimum-Cost Flow library specialized for the data and topology of the Lightning Network to be used within Pickhardtpayments package to compute reliable Multi-part payments in the Lightning Network. My library doesn’t have any dependency and for every payment size it performs faster than the current code that uses OR-tools’ MCF solver. This is mostly due to the design of the underlying data structures that allow to have a dynamic representation of the uncertainty network graph and thus we avoid unnecessary data transfering between iterations of Pickhardtpayments. In the processes of testing my library I’ve discovered that the topology of the LN is such that augmenting-path (successive shortest path) algorithm performs better than cost-scaling for payment amounts below 1M sats.
References
[1] www.summerofbitcoin.org
[2] Rene Pickhardt, Stefan Richter. Optimally Reliable & Cheap Payment Flows on the Lightning Network https://arxiv.org/abs/2107.05322
[3] https://lagrang3.github.io/2022-08-19-pickhardtpayments
[4] https://github.com/renepickhardt/pickhardtpayments
[5] R.K. Ahuja, T.L. Magnanti, and J.B. Orlin. Network Flows: Theory, Algorithms, and Applications. Prentice Hall, 1993.
[6] https://developers.google.com/optimization/flow/mincostflow?hl=en#python
[7] Andrew V. Goldberg, Robert E. Tarjan, (1990) Finding Minimum-Cost Circulations by Successive Approximation. Mathematics of Operations Research 15(3):430-466. http://dx.doi.org/10.1287/moor.15.3.430
[8] https://github.com/Lagrang3/mincostflow
[9] Andrew V Goldberg. An Efficient Implementation of the a Scaling Minimum-Cost Flow Algorithm. Journal of Algorithms, Volume 22, Issue 1, Jan. 1997 pp 1–29, https://doi.org/10.1006/jagm.1995.0805
[10] https://networkx.org/
[11] https://github.com/renepickhardt/pickhardtpayments/pull/29