Since version v23.08 core-lightning [1] comes with an implementation of Pickhardt-Richter algorithm for payment routings in the lightning network. This comes in the form a new plugin called renepay.

In a previous post I have explained the ideas, to my understanding, of the method [2]. This is the first of a series of posts explaining the design choices for the implementation of renepay. In this post I am going to explain how the linearization of the cost function was performed. I am writing this post to help reviewers and maintainers go through the code.

Notation and conventions

The lightning network can be represented as a directed graph \((G,E)\) where \(G\) is the set of all lightning routing nodes and \(E\) is the set of directed channels. Whenever there exist a channel between a pair of nodes \(N_1, N_2 \in G\) there are two corresponding directed arcs in \(E\) corresponding to parts of that channel that can forward payments from \(N_1\) to \(N_2\) and from \(N_2\) to \(N_1\) respectively. In core lightning these arcs are uniquely identified with a pair (idx,dir), where idx is an u32 index for the channel and dir is an int that can take values either 0 or 1 to indicate the arc’s direction.

Uniform Probability Distribution model

Pickhardt-Richter method is in its most general form assuming we can describe the liquidity of the directed channel \(e\in E\) as a random variable \(\hat X_e\).

In a first approach to the routing problem one can assume that \(\hat X_e\) follows a Probability Distribution Function (PDF) which is uniform, so that the state of a channel can be constrained by a pair of numbers \([a_e,b_e)\) meaning that the liquidity satisfies \(a_e \le \hat X_e < b_e\) with non-zero probability and any value for the liquidity in this range has the same probability of occurring. As a side note: there is room for improvement in this method, since the uniform PDF is only a conjeture and there are likely better models to describe \(\hat X_e\) given the dynamics of liquidity in the lightning network. In other words: it doesn’t have to be uniform, we just assume it is, and as a matter of fact this assumption is fair because it reflects our current knowledge/ignorance.

A directed channel can forward a payment of value \(x\) if the liquidity is greater or equal than it, therefore in the case of the uniform PDF we obtain:

\[P(\hat X_e \ge x) = \begin{cases} 1, & x \lt a_e \\ \frac{b_e - x}{b_e - a_e}, & a_e \le x \lt b_e\\ 0, & x\ge b_e \end{cases}\]

Pickhardt-Richter method then consists in finding a set of payment routes that maximizes the probability of success of the payment (a multiplication of probabilities of success for each forwarding channel). The cost function that separates these probabilities is minus the logarithm of the probability (see the previous post [2] or the paper [3] for details)

\[c_e(x) = - \log P(\hat X_e \ge x)\]

And the optimization of the success probability transforms to a problem of finding a Flow on the graph that forwards the payment amount with the least cost—not fees in our case, but cost in terms of probabilities. The smaller the cost of the flow the more likely is the payment to go through.

Piecewise linearization of the cost function

If the cost function was linear, the optimization of the success probability could be efficiently performed using well known Minimum Cost Flow (MCF) algorithms. Therefore, one possible approach to the problem consists in performing a piece-wise linearization of the cost function and build a new graph where each arc correspond to one of those linear cost pieces.

The approximation will be better if there are many such channel pieces, but it will also have a higher computational cost for the MCF algorithm, hence we try to keep the number of pieces small.

Also, we have the freedom to choose where pieces are placed. I argue that it would not make sense to set the pieces at fixed values of the flow because it might work well for some channels but it will work terrible for others. For instance, let’s suppose we choose that the first piece goes from 0 sats to 1000 sats, then that would certainly correspond to a linear function for channels with lower liquidity bound \(a\) greater than 1000 sats for which the cost is 0 in this region, but for a channel with upper bound \(b = 500\) sats this linearization is undefined since the cost goes to infinity at \(500\) sats. This little example suggests that we should choose a different piece linearization for each directed channel and the pieces are to be choosen relative to the liquidity bounds \([a,b)\). That is, choose the first piece from 0 to \(a\), the second piece starting from \(a\) but with a length which is a fraction of the \(b-a\), the next piece starts at the end of the previous piece and the length is a fraction of the remaining distance to \(b\), and so on, but stop before getting to \(b\), where costs becomes undefined.

The idea is equivalent to define a new variable \(t = \frac{x-a}{b-a}\), \(t\) is also the probability of failure for a given flow \(x \ge a\). With this transformation the interval \([a,b)\) is mapped into \([0,1)\). Then linearize the cost function \(c(t) = - \log (1-t)\) in the \(t\)-domain, then come back to the \(x\)-domain with a linear transformation. Clearly a linear function in \(t\) is also linear in \(x\). In the upside, with this strategy every directed channel have the same cost function, i.e. the \(a,b\) dependence is washed out by the \(x \to t\) transformation. Figure 1 shows the cost function in terms of \(t\).

Fig. 1 - Cost as a function of the fail probability. t=0 corresponds to a flow x=a and t=1 corresponds to a flow x=b.

In the current implementation of renepay we have chosen the following pivot points (in value of \(t\)) for the linearization: 0, 0.5, 0.8, 0.95. We can refer to these points as \(t_0 = 0, t_1 = 0.5, t_2 = 0.8\) and \(t_3 = 0.95\). Notice that this choice is arbitrary and further research on the topic could be aimed at finding better pivots.

The table below shows the computation of the slope of the piece-wise linearization for the aforementioned pivots.

Range \([t_{n-1},t_n)\) \(\Delta t\) \(\Delta c = - \log(1-t_{n}) + \log(1-t_{n-1})\) \(\Delta c / \Delta t\)
below 0 - 0 0
[0,0.5) 0.5 0.69 1.38
[0.5,0.8) 0.3 0.92 3.05
[0.8,0.95) 0.15 1.39 9.24

The slope in the \(x\)-domain is easily computed as

\[\frac{\Delta c}{\Delta x} = \frac{\Delta c}{\Delta t} \frac{\Delta t}{\Delta x} = \frac{\Delta c}{\Delta t} \frac{1}{b-a}\]

while the capacity of the arc pieces is \(\Delta t \cdot (b-a)\).

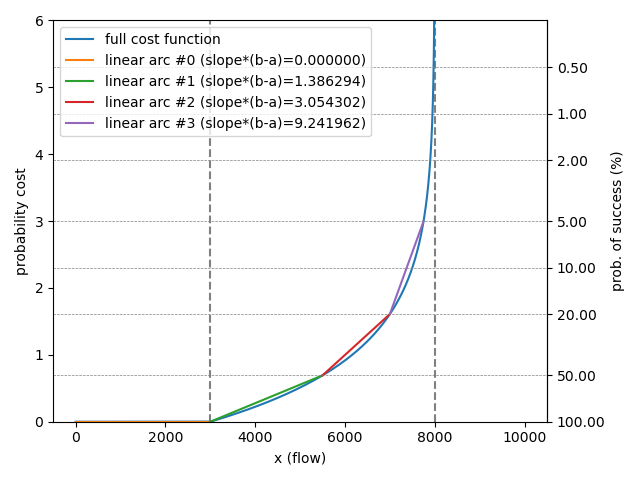
For example, let’s linearize a channel with liquidity in the range \([3000,8000)\):

  • the first linear cost arc starts at \(x=0\) and ends at \(x=a = 3000\), thus this arc has a capacity equal to \(a-0 = 3000\), the cost is constant and equal to zero hence this arc’s slope is \(m = 0\);

  • the second arc starts where the previous arc stopped, at \(x = a = 3000\) and ends at \(x = a + (b-a)\cdot t_1\), thus the capacity is equal to \(t_1\cdot (b-a) = 2500\), and a slope of \(1.38/(b-a) = 0.000276\);

  • the third arc starts where the previous arc stopped and ends at \(x = a + (b-a)\cdot t_2\), thus the capacity is equal to \((t_2 - t_1)\cdot (b-a) = 1500\) and the slope is \(3.05 / (b-a) = 0.00061\);

  • the fourth arc starts where the previous arch stopped and ends at \(x = a+ (b-a)\cdot t_3\), the capacity is equal to \((t_3 - t_2)\cdot (b-a) = 750\) and the slope is \(9.24 / (b-a) = 0.001848\).

Figures 2 and 3 show two examples of piece-wise linearization for two channels with liquidity bounds [3000,8000) and [0,10000) respectively. It should be noticed that the cost function depends on the parameters \(a\) and \(b\) but both functions are similar under a linear transformation (a shift and a squeeze). With our linearization scheme the pieces with non-zero cost correspond always to the ranges of success probability: from 100% to 50%, from 50% to 20% and from 20% to 5%, this is not a coincidence, this is because we have chosen pivots in \(t\) at \([0,0.5,0.8,0.95]\) which correspond to those points where the probability of success \(1-t\) acquires the values \([1,0.5,0.2,0.05]\) respectively.

Fig. 2 - Linearized cost for a channel with bounds [3000,8000).
Fig. 3 - Linearized cost for a channel with bounds [0,10000).

Discussion

The cost function for the implementation of renepay in core-lightning depends on two design choices that are open for future improvements:

  1. the PDF for the state of the liquidity in each channel, that is currently modelled as a uniform PDF dependent on two parameters \(a\) and \(b\) that encode the bounds for knowledge of liquidity, i.e. liquidity is uniformly distributed in the range \([a,b)\).

  2. a piece-wise linearization of the cost function that is performed in the space of the probability of failure \(t = \frac{x-a}{b-a}\), at the selected pivots \([0,0.5,0.8,0.95]\). Fewer pieces mean less overhead in the MCF computation (because there are less arcs) but less precision in the approximation of the cost function. In our opinion 4 arcs (or pieces) per directed channel is a good compromise, it is also a power of two so these arc indexes can be encoded exactly in 2 bits.

A drawback in our choice is that due to the last pivot value of 0.95, it follows that \(0.05\cdot (b-a)\) of the liquidity of the channel will not be avaible for routing. However, by definition, this capacity region has success probability of at most 5%, and one might argue that it is anyways not suitable for practical use.

References

[1] https://github.com/ElementsProject/lightning

[2] Pickhardt payments in the Lightning Network on this site.

[3] Rene Pickhardt, Stefan Richter. Optimally Reliable & Cheap Payment Flows on the Lightning Network https://arxiv.org/abs/2107.05322