Renepay II

Introduction

In an optimization problem with two features \(A\) and \(B\), with respective cost functions \(C_A(x)\) and \(C_B(x)\). If we combine the costs of the features linearly, ie. such that any solution to the problem \(x\) has a cost \(C(x) = C_A(x) + C_B(x)\), we are implying that each cost unit of feature \(A\) is worth one cost unit from feature \(B\). If an optimal solution exists \(x_o\) it is implied that any solution that satisfies \(C(x') = C(x_o)\) is as good from the point of view of the algorithm, thus any solution that satisfies \(C(x) = C(x_o)\) could be found. So for instance if we know the optimal solution achieves \(C(x_o) = 1.0\) any solution \(x_1\) with \(C_A(x_1)=0.2\) and \(C_B(x_1)=0.8\) is as good as any other solution \(x_2\) with \(C_A(x_2)=0.5\) and \(C_B(x_2) = 0.5\).

Let’s make an example: suppose we are planning for a battle strategy, we use a computer to find an strategy \(x\) such that we minimize our losses. In order to quantify losses we define feature \(A\) as the expected number of airplane lossess and \(B\) as the number of tank losses. The cost of the features is the amount of USD worth of losses. So \(C_A(x) = p_A \cdot A(x)\), where \(p_A\) is the price of a single airplane and \(C_B(x)=p_B\cdot B(x)\) is the price of a single tank. The total cost function can be constructed as \(C(x) = p_A\cdot A(x) + p_B\cdot B(x)\), because one airplane dollar is as good as one tank dollar. If a tank is valued at \(p_B = 100k\) and an airplane is valued as \(p_A = 1M\), a solution in which 1 aiplane and 0 tanks are lost is as good as another solution with 0 airplanes losses but 10 tanks are lost. You wouldn’t want to define the cost as \(C(x) = A(x) + B(x)\) because an airplane is worth 10 times more than an tank, so a solution with \(A = 1\) and \(B=0\) is a worst loss than \(A=0\) and \(B=1\), even though \(A+B=1\) stays the same.

In general we can estimate how many units of feature \(A\) are worth in terms of feature \(B\) we just need to make the partial derivatives of the combined cost function at the region of optimality:

since \(C\) is constant in this region we have \(\delta C = 0\) and we obtain

the minus sign just indicates that one feature cost must increase for the other feature cost to decrease in order to remain in the optimality region.

In the airplanes vs tanks examples the costs are linear functions, therefore we obtain

Thus, one tank is worth as much as 0.1 airplane, or 1 airplane is worth as much as 10 tanks.

Renepay cost function

In renepay we had two main features to minimize: the probability of failure \(p\) and the fees \(f\). The cost function for the probability of failure is \(C_p(x) = -\log(1-p(x))\) and the cost function of the fee is the fee itself \(C_f(x) = f(x)\). We proposed a combined cost function of the form:

where \(k\) is a constant which is unspecified. The cost function must combine fees and uncertainty cost linearly in order to be able to use Minimum Cost Flows (MCF) algorithms to find an optimal solution, but also the linear combination seems a reasonable choice.

In an scenario where there are no fees, an optimal solution will optimize the probability regardless of the value of \(k\) (as long as \(k>0\)). Therefore the only true significance of \(k\) is to combine fees and uncertainty cost. When \(k\) is fixed by hand, it is implicitely carrying information about the tradeoffs of fee and reliability (probability) we are willing to take for an optimal solution. How much in fees are worth the probability units is given by the following expression once we take partial derivatives of the cost function:

For instance if \(k\) was 1 sat and if the optimal solution lies around \(p \approx 0\) (almost certain success) then \(1\%\) in probability is worth \(0.01 \times k = 100 \,\mathrm{msat}\) in fees.

Finding a candidate for k

One might argue that having \(k\) fixed is not a good approach simply because the bigger the payment size, the payer might be willing to pay more fees in exchange of reliability. So we proposed to write \(k\) as the multiplication of the payment amount \(T\) and a fraction \(\alpha / 10^6\), with \(\alpha\) some integer number between 1 and \(10^6\), in other words: parts per million.

With this choice it follows that each unit of uncertainty is worth not a fixed amount of sats, but a fraction of the payment amount:

For example let \(\alpha = 1000\), then for an optimal solution, assuming \(p \approx 0\) every \(0.1\%\) of certainty gained is worth 1 PPM of the payment amount that goes into fees. In the current implementation [1] there’s an extra factor called prob_cost_factor with default value 10, that multiplies the uncertainty cost. Thus the interpretation of prob_cost_factor is the number of PPM in equivalent fees that we are willing to pay for each \(0.1\%\) of improvement in the probability of success.

After linearization

In a previous post [2] I have explained how linearization of the uncertainty cost function is performed in renepay in order to be able to apply linear MCF algorithms to optimize the payment. A channel with liquidity in the range \([a,b)\) was split into 4 arcs. The zeroth arc comprises the liquidity range with total certainty in the range \([0,a)\), the consecutive arc split the liquidity region where all uncertainty lies in \([a,b)\), see for example figure 1:

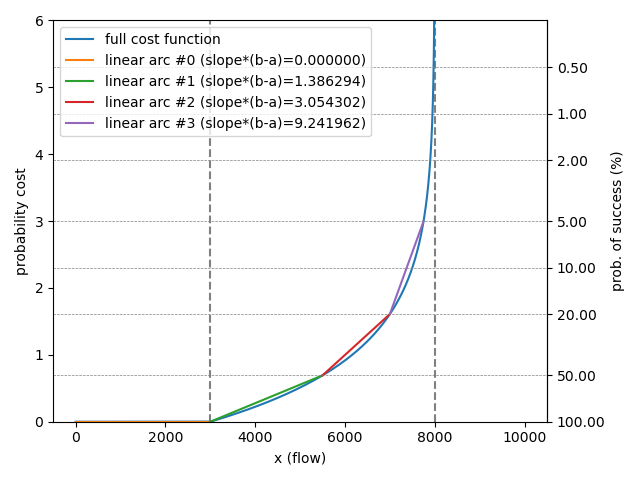
The slopes of the linearized uncertainty cost function are always a constant factor divided by the conditional capacity \(b-a\).

When we consider this linearization combined with our choice for the weight factor k, we obtain for each linearized arc the following cost per unit of flow:

where \(m\) is the linearized cost slope for a conditional capacity of 1, ie. \(m = 1.38, 3.05, 9.24\) depending on the index of the arc.

For our MCF algorithm we work exclusively with integer numbers. So that cost per unit of flow is an integer, the flow unit is an integer and thus the cost is again an integer number. This gives us limited precision. So for instance if the flow is in units of sats and the cost per unit of flow is adimentional, we obtain a cost in sats. But a cost in sats will not be able to measure a cost per unit of flow of the order of the PPM, which is the usual reference unit for the proportional_fee. So we have chosen to measure the cost in micro-sats instead. This is achieved by multiplying the whole cost function by the sats to micro-sats ratio of 1M. Therefore the actual integer cost per unit of flow [3] is

This cost per unit of flow becomes zero (beyond our precision) if the amount \(T\) falls below \((b-a)/1000\), assuming we have choosen the smallest value of prob_cost_factor=1 and taking \(m\approx 1\):

Which corresponds in the worst case to a channel that tries to forward the entire amount \(T\) through it’s conditional capacity \(b-a\), and it does with a probability of failure \(p \approx T/(b-a) = 10^{-3}\), which is pretty much negligible and thus a zero uncertainty cost per unit of flow for this channel is acceptable. Furthermore, if the prob_cost_factor is even bigger, for example prob_cost_factor=10 we get even a smaller limit in precision to \(p \approx 10^{-4}\). In other words: channels with a failure probability of forwarding the entire payment \(p(T)\) that fall below \(10^{-3}/\mathtt{prob\_cost\_factor}\) have a zero uncertainty cost.

References

[1] pay.c Line 782

[2] Renepay I on this site.

[3] mcf.c Line 491